ISBN Information
Anatomy of a 13-digit ISBN
The 13-digit ISBN was introduced in the fourth edition of ISO standard 2108, of May 2005, to be in use for all new ISBNs from 1st January 2007. To understand the following fully, it may be necessary to be familiar with the 10-digit ISBN from which the 13-digit ISBN was developed. For details of the 10-digit ISBN, see the Anatomy of a 10-digit ISBN page.
If you are interested in how the ISBN barcode works, in detail, then see the ISBN barcode page.
The 13-digit ISBN came about from the reorganization that resulted from the fourth edition of the standard ISO 2108 that defines the ISBN system. This revision mainly prevents the number of new ISBNs running out in the near future, but also integrates the ISBN system into the wider system of product numbering known as EAN which also uses 13-digits for a whole range of goods. For further details of the history of the ISBN system, see the History of the ISBN system page.
We will take an example of a 13-digit ISBN to use in the discussion that follows. The example is taken from the book "Why Don't Penguins' Feet Freeze: and 114 other questions", edited by Mick O'Hare and published by Profile Books in 2006.

When you look at the ISBN as printed above the barcode on the book shown in the photographs taken of the back cover and from the back of the title page near the front of the book, you can see it is separated into sections by hyphens or by spaces.
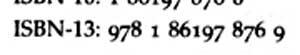
These photographs show the ISBN like this:
ISBN-13: 978-1-86197-876-9 ISBN-13: 978 1 86197 876 9
The actual ISBN (9781861978769) has been separated into groups by hyphens or spaces just to make it easier for humans to be aware of the different sections of the particular ISBN.
There are five groups of numbers, whereas the 10-digit ISBN had four groups. The same four groups are present in the 13-digit ISBN as were present in the 10-digit ISBN, although they are given somewhat different names in the new edition of the standard to that in the 10-digit standards. The extra group present in the 13-digit ISBN is the first one, a 3-digit identifier called the "prefix element".
The five groups from left to right are:
- Prefix element
- Registration group element
- Registrant element
- Publication element
- Check digit
Prefix element
The first, leftmost element, of an ISBN, apart from the designator "ISBN-13:", is the prefix element. It is always three characters long. This element in effect makes an ISBN into the universal product code known as an EAN, ensuring that the ISBN system is integrated into the wider system of product identification that is administered by the EAN system. For further details of the EAN system, see the The EAN system explained page.
The prefix element is made available to the ISBN system by GS1, the global standards organisation, formerly part of which was EAN International.
In the EAN system, this 3-digit prefix is used to refer to the country of origin of a product, for ISBNs this prefix refers to the fictitious country of Bookland. You may see an ISBN referred to as a Bookland ISBN. This refers to the 13-digit EAN that results when a pre-2007 10-digit ISBN is converted to a 13-digit EAN code. A further element of the ISBN is concerned with a book's geographical origin.%p Currently, the only possible prefix elements for ISBNs are 978 and 979. For our sample book, the prefix element is 978:
ISBN-13: 978
Registration group element
The registration group element is the second section of a 13-digit ISBN and refers to the country, geographical area, or language area of the book. It is identical to the group identifier in a 10-digit ISBN.%p For our example book, the registration group element is 1:
ISBN-13: 978-1
Registrant element
The registrant element is the third section of a 13-digit ISBN and refers to the publisher or imprint issued that identifier within the registration group. It is the same as the publisher identifier in a 10-digit ISBN.
For our example book, the registrant element is 86197:
ISBN-13: 978-1-86197
Publication element
The publication element is the fourth element of a 13-digit ISBN and refers to the specific publication by that registrant within that registration group. It is the same as the title identifier in a 10-digit ISBN.
For our example book, the publication element is 876:
ISBN-13: 978-1-86197-876
Check digit
The check digit completes the 13-digit ISBN and performs the same function as the check digit in a 10-digit ISBN, and is calculated in a similar way, with some major detail differences.
For our example book, the check digit is 9:
ISBN-13: 978-1-86197-876-9
Check digit calculation
You should familiarise yourself with the check digit calculation for a 10-digit ISBN, before reading the following. See the Anatomy of a 10-digit ISBN page for details.
Instead of using weights of 10 through to 2 as in the check digit calculation for the 10-digit ISBN, the calculation for the 13-digit ISBN uses weights of 1 and 3 alternately, six times over, for the 12-digits prior to the check digit. The product of the weight and the digit of the element is taken, and the resulting products are added together, just as in the 10-digit ISBN calculation.
The result number has 10 taken from it as many times as may be wholly done, like the 10-digit ISBN calculation where 11 was used. This may result in a remainder of between 0 and 9. If it is 0, then the check digit is 0, otherwise the check digit is 10 minus the remainder.
The calculation is shown below for the example book, the ISBN for the first four sections of it being 978186197876.
| Calculating a Check Digit | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ISBN | 9 | 7 | 8 | 1 | 8 | 6 | 1 | 9 | 7 | 8 | 7 | 6 | |||||||||||||
| Weight | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | |||||||||||||
| Product | 9 | + | 21 | + | 8 | + | 3 | + | 8 | + | 18 | + | 1 | + | 27 | + | 7 | + | 24 | + | 7 | + | 18 | = | 151 |
151 divided by 10 = 15 remainder 1 The check digit is 10 - 1 = 9
Another way to complete the calculation is to take the sum from the weighting products (151) and simply see how many would need to be added to the number to make it up to the next exact multiple of 10 (which in this case would be to add 9 to get to 160).
To get from 151 to 160 takes 9 The check digit is 9
Check digit validation
It is possible to validate a complete 13-digit ISBN, one that includes its check digit, by a similar procedure to calculating the check digit. Simply perform the same calculation, adding the check digit to the calculated product with a weighting of one. When the division by ten is performed, the remainder will be zero for a valid ISBN. Please note that the validation being performed here is to check the correctness of the check digit for the rest of the numbers and their place in the number. This does not mean, necessarily, that this ISBN has ever been issued to a book, or that it is valid in a number of other ways.
| Validating a Check Digit | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ISBN | 9 | 7 | 8 | 1 | 8 | 6 | 1 | 9 | 7 | 8 | 7 | 6 | 9 | ||||||||||||||
| Weight | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | ||||||||||||||
| Product | 9 | + | 21 | + | 8 | + | 3 | + | 8 | + | 18 | + | 1 | + | 27 | + | 7 | + | 24 | + | 7 | + | 18 | + | 9 | = | 160 |
160 divided by 10 = 16 remainder 0 Zero remainder = valid ISBN
Another way to complete that check is to take the sum from the weighting products (160) and simply see if it is an exact multiple of 10.
160 is an exact multiple of 10, so the ISBN number has passed the test.